1. Расчет характеристик самонесущего оптического кабеля
1.1. Начальный модуль упругости
При растяжении кабеля необходимо учитывать модуль упругости кабеля, Eкаб. Оптический кабель состоит из различных материалов, при этом определяющее значение на модуль упругости целого кабеля оказывают центральный силовой элемент и упрочняющие нити.
Для расчета модуля упругости кабеля, необходимо воспользоваться следующей формулой:
где Ei и Si – модуль и площадь i-го несущего элемента кабеля.
Понятно, что модуль упругости кабеля также зависит от числа и вида силовых элементов и определяется изготовителем кабеля.
1.2. Сечение кабеля
Расчет производится по следующей формуле:
где Dкаб – внешний диаметр кабеля.
Необходимо учесть, что модули упругости приведены к сечению всего кабеля в целом. Соответственно приводится и расчет площади всего кабеля. В этом случае расчет площади твердых элементов кабеля не нужен.
1.3. Расчет максимально допустимой растягивающей нагрузки
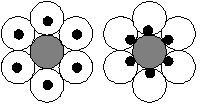
При расчете рассматриваются оптические кабели со свободной укладкой волокна в оптических модулях скрученных вокруг центрального силового элемента (ЦСЭ) (типов ДПТа, ДПТс, ДОТа, ДОТс производства ООО «Инкаб»). Максимально допустимая растягивающая нагрузка пропорционально предельно допустимому удлинению самого кабеля и оптического волокна. Удлинение кабеля приводит к тому, что волокна, расположенные в центре модуля, начинают смещаться к внутренней поверхности модуля у ЦСЭ (рис. 1):
Рис. 1. Расположение волокон в оптическом модуле.
При этом еще не происходит удлинения волокна. При дальнейшем удлинении волокно распрямляется за счет избыточной длины в модуле. После распрямления начинает удлиняться само волокно, при этом оно не должно превысить некоторого допустимого значения. Поэтому допустимое удлинение кабеля вычисляется по следующей формуле:
где, εдоп — максимально допустимое удлинение кабеля; εк — допустимое удлинение кабеля, при котором волокно не подвергается механическому напряжению; εизб — избыточная длина волокна в модуле; εов — максимально допустимое удлинение оптического волокна.
Избыточная длина волокна в модуле закладывается при его изготовлении и задается изготовителем ОК. Максимально допустимое удлинение оптического волокна определяется исходя зависимости срока службы оптического волокна от приложенной растягивающей нагрузки. При определенном сроке службы кабеля в 25 лет, допускается удлинение волокна на величину до 0,25% без ухудшения его свойств в течение всего времени. Следует понимать, что максимально допустимая растягивающая нагрузка действует на кабель максимум несколько суток раз в 10–15 лет, что также гарантирует сохранение свойств волокна в течение всего срока службы. Допустимое удлинение кабеля, при котором волокно не подвергается механическому напряжению, зависит от конструкции, определяемой конкретным изготовителем, и рассчитывается по следующей формуле:
где, R — радиус скрутки; S — шаг скрутки; ΔR — зазор между оптическим волокном и внутренней стенкой модуля.
Путем увеличения радиуса скрутки и зазора (внутреннего пространства модуля), а также уменьшения шага скрутки можно получить большее допустимое удлинение кабеля без механического напряжения волокна. При этом шаг скрутки не должен быть меньше определенной величины, определяемой минимальным радиусом кривизны волокна за счет спиральной скрутки модулей. Таким образом, зная начальный модуль упругости кабеля, его сечение и допустимое удлинение, можно определить максимально допустимую растягивающую нагрузку на кабель (МДРН):
Именно эта расчетная величина, указывается изготовителем в характеристиках кабеля. Соответственно, при расчете нагрузок, действующих на кабель при заданных условиях эксплуатации необходимо, чтобы они не превышали МДРН кабеля.
1.4. Прочие допустимые нагрузки
Допустимая монтажная нагрузка (ДМН) — нагрузка, которая допустима при монтаже кабеля и его прокатке через ролики.
Максимально допустимая монтажная нагрузка (МДМН) — нагрузка, которая допустима при выставлении монтажных стрел провеса.
Разрывная нагрузка — нагрузка, при которой происходит разрыв кабеля.
Значения данных нагрузок зависят от механических свойств кабеля, как совокупности конструкции и материалов (в первую очередь количества силовых элементов), а, следовательно, пропорциональны значению МДРН.
1.5. Масса кабеля
Рассчитывается как масса отдельных материалов из которых состоит кабель:
где
— массы центрального силового элемента, оптических волокон, ПБТ, корделей, гидрофобов внутримодульного и межмодульного, промежуточной оболочки, силовых нитей и наружной оболочки соответственно.
1.6. Наружный диаметр кабеля
Рассчитывается следующим образом:
Где Dскр — диаметр по скрутке, который складывается из диаметра центрального силового элемента и диаметров оптических модулей; hпр.об. — толщина промежуточной оболочки (при ее наличии); hнить — толщина слоя силовых нитей; hоб. — толщина наружной оболочки.
1.7. Конечный модуль упругости
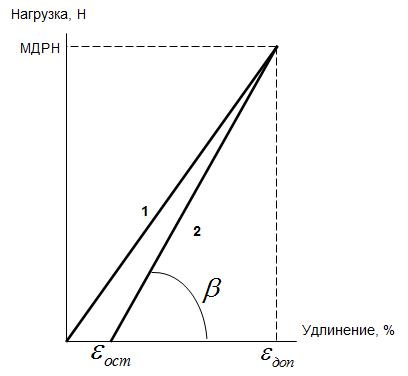
Первоначальное удлинение оптического кабеля при увеличении прикладываемой нагрузке происходит по начальному модулю упругости. Однако после снятия максимальной нагрузки, в кабеле остается остаточное удлинение (см. рис):
Далее растяжение-сжатие происходит по прямой 2 на рисунке, соответственно расчет нужно проводить по конечному модулю упругости, определяемому как тангенс угла между получившейся прямой 2 и осью удлинения. Для определения конечного модулей упругости необходимо провести тест на растяжение-сжатие. К кабелю прикладывается растягивающая нагрузка, возрастающая до МДРН. Параллельно фиксируется удлинение кабеля. Далее растягивающая нагрузка снимается и фиксируется остаточное удлинение. Точка на графике, соответствующая этому растяжению, соединяется с точкой, соответствующей МДРН и максимально допустимому удлинению кабеля. Тангенс угла между получившейся прямой 2 и осью удлинения будет равен конечному модулю упругости:
где εдоп — остаточное удлинение кабеля.
1.8. Модуль упругости после вытяжки
При расчетах необходимо учитывать вытяжку кабеля при среднеэксплуатационной нагрузке. Вытяжка кабелей имеет место для всех типов кабелей, в независимости от материала армирующих элементов. Величина вытяжки определяется как свойствами кабеля, так и величиной растягивающей нагрузки. При проектировании подвески кабеля необходимо рассчитывать стрелы провеса и тяжения кабеля с учетом его вытяжки при среднеэксплуатационной нагрузке, которая не всегда бывает определяющей в эксплуатации, а также и в режиме после воздействия максимальной внешней нагрузки, воздействие которой, может приводить к большей остаточной деформации кабелей.
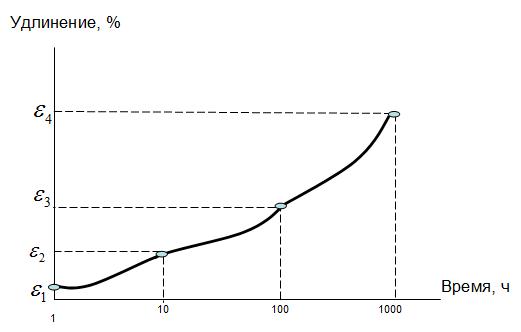
Условия, при которых удлинение кабеля будет наибольшим при его эксплуатации, определяются условиями подвески (длина пролета, стрела провеса, внешние климатические нагрузки) и физико-механическими параметрами кабеля. Для определения модуля упругости после вытяжки проводят тест на вытяжку в соответствии с IEEE 1222. К кабелю прикладывается растягивающая нагрузка, равная 50% МДРН. При этом температура должна оставаться постоянной. Регистрируются удлинения кабеля через 1, 10, 100 и 1000ч.
Получившийся график зависимости вытяжки от времени описывается функцией:
где ε — удлинение кабеля; t — время, ч; A, B — коэффициенты, вычисляемые из эксперимента. Коэффициент А определяется как вытяжка, зафиксированная через 1 час после начала эксперимента. Коэффициент В определяется путём подстановки в уравнения текущего значения вытяжки, времени и известного значения коэффициента А:
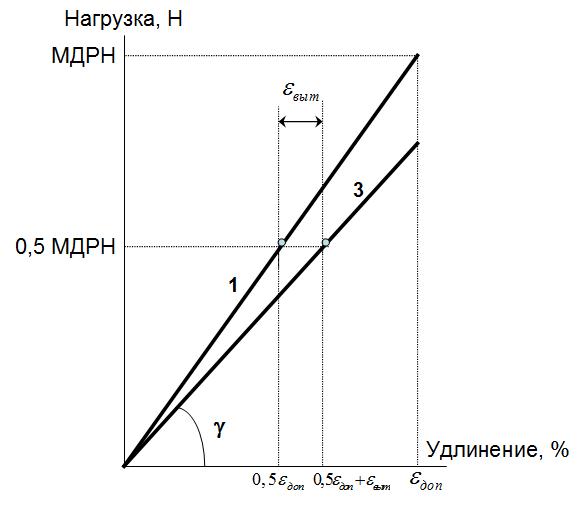
Зная коэффициенты А и В, можно вычислить величину вытяжки кабеля через 25 лет при значении нагрузки 50% от МДРН. Через соответствующую точку можно построить зависимость удлинения от нагрузки для СОК при учёте 25 летней вытяжки.
Тангенс угла между получившейся прямой и осью удлинения будет равен модулю упругости после вытяжки:
где εвып. — удлинение СОК после 25 летней вытяжки.
1.9. Минимально допустимый радиус изгиба кабеля
Определяется по следующей формуле:
1.10. Температурный коэффициент линейного расширения
ТКЛР всех элементов в кабеле (кроме арамидных нитей) имеет положительное значение.
ТКЛР арамидных нитей имеет отрицательное значение.
ТКЛР всего кабеля будет определяться исходя из условия равновесия всех элементов, входящих в кабель, по следующей формуле:
где — ТКЛР каждого элемента кабеля.
1.11. Температуры эксплуатации и монтажа
Температурный диапазон эксплуатации определяется исходя из требований, указанных в «Правилах применения оптических кабелей связи, пассивных оптических устройств и устройств для сварки оптических волокон», утвержденных Приказом Мининформсвязи России № 47 от 19.04.2006г. Минимально допустимая температура монтажа определяется исходя из проведенных испытаний на изгиб кабеля при отрицательных температурах и обеспечивается соответствующими применяемыми материалами и технологией производства.
1.12. Максимально допустимый потенциал электрического поля
Максимально допустимый потенциал электрического поля определяется исходя из типа материала применяемого в оболочке.
Обычный полиэтилен средней или высокой плотности в оболочке допускает максимальное воздействие потенциала электрического поля в 12 кВ.
Трекингостойкий полиэтилен в оболочке допускает максимальное воздействие потенциала электрического поля в 24 кВ.
2. Расчет стрел провеса и нагрузок при различных климатических условиях
2.1. Вес кабеля
Вес кабеля в Н/м рассчитывается исходя из заданной массы кабеля кг/км по следующей формуле:
Где g – ускорение свободного падения, м/с2.
2.2. Растягивающая нагрузка, действующая на кабель
Растягивающая нагрузка, H, действующая на кабель вычисляется следующим образом:
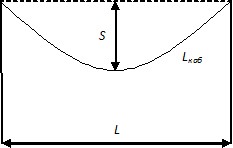
где W — линейный вес кабеля, Н/м; L — расстояние между опорами, м; S – стрела провеса, м — определяемая как максимальная величина, на которую провисает кабель от горизонтальной линии между точками подвеса кабеля.
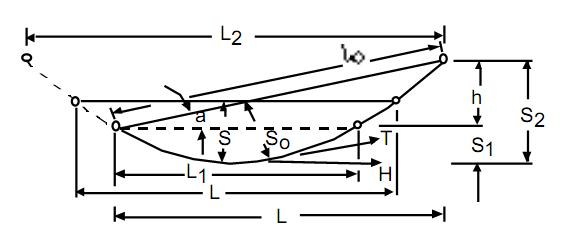
Исходя из формулы, видно, что нагрузка на кабель увеличивается с увеличением веса кабеля и расстояния между опорами и уменьшается при увеличении стрелы провеса. Начальная нагрузка на кабель:
2.3. Перепад высот между опорами
При разной высоте точек подвеса, кривая провисания кабеля будет несимметричной и низшая точка этой кривой будет находиться не посередине, а ближе к более низкой опоре. В данном случае, для расчета стрел провеса удобно пользоваться значениями эквивалентных пролетов.
Можно достроить левую ветвь кривой до точки, одинаковой по высоте с правой, и получить симметричную кривую. Расстояние L1 называется малым эквивалентным пролетом, а расстояние L2 – большим эквивалентным пролетом. Расстояния L1 и L2 рассчитываются следующим образом:
Стрелы провеса S1 и S2:
Где h – перепад высот между точками подвеса кабеля, м. В случае подвеса кабеля на одном уровне L1=L2=L и S1=S2=S.
2.4. Длина подвешенного кабеля
Очевидно, что длина подвешенного кабеля больше расстояния между опорами, за счет некоторого провеса кабеля и она, тем больше, чем больше стрела провеса. Длина подвешенного кабеля рассчитывается следующим образом:
2.5. Длина кабеля в ненагруженном состоянии
Для дальнейших расчетов необходимо знать длину кабеля между опорами, как если бы он не находился под действием растягивающих нагрузок (H = 0). Данная величина называется длиной кабеля в ненагруженном состоянии, Lн0:
2.6. Длина кабеля в ненагруженном состоянии с учётом температуры
Дальше необходимо определить длину кабеля в ненагруженном состоянии с учетом температуры кабеля, Lнк. Под действием температуры кабель может, как удлиняться, так и сжиматься и эта способность определяется температурным коэффициентом линейного расширения кабеля (ТКЛР, 1/°С).
где Т — температура кабеля в условиях эксплуатации; Тср — средняя температура эксплуатации.
2.7. Вес кабеля при воздействии максимального гололёда
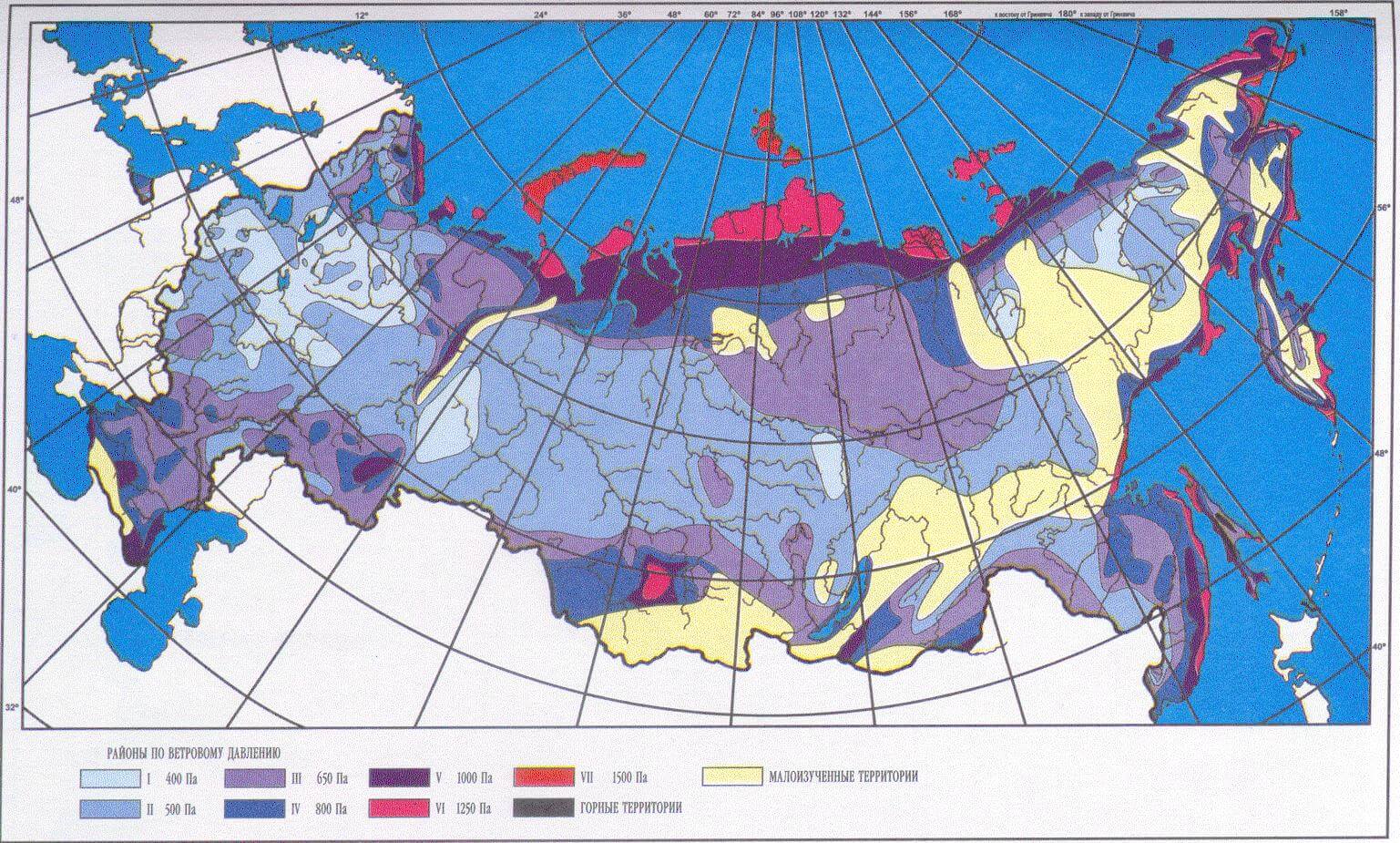
В некоторые периоды эксплуатации происходит обледенение оптического кабеля подвешенного между опорами. При этом величина обледенения зависит от географического местоположения подвешенного кабеля и определяется районами гололедности по классификации и картам гололедных районов РФ, согласно Правилам устройства электроустановок (ПУЭ) — 7 ред. Гололедная нагрузка действует на кабель вертикально вниз. Исходя из заданного района гололедности определяют толщину стенки льда на кабеле и рассчитывают вес кабеля в условиях обледенения:
Где ρл — объемная масса гололеда (обычно 0,9·10-3), кг/см3; С — толщина стенки гололеда, мм; d — диаметр кабеля, мм; Ki и Kd — коэффициенты учитывающий изменение толщины стенки гололеда по высоте и в зависимости от диаметра провода. Коэффициенты Ki и Kd учитывающие изменение толщины стенки гололеда:
| Высота расположения приведенного центра тяжести проводов, тросов и средних точек зон конструкций опор над поверхностью земли, м | Коэффициент Ki, учитывающий изменение толщины стенки гололеда по высоте над поверхностью земли |
| 25 | 1,0 |
| 30 | 1,4 |
| 50 | 1,6 |
| 70 | 1,8 |
| 100 | 2,0 |
| Диаметр провода (троса), мм | Коэффициент Kd, учитывающий изменение толщины стенки гололеда в зависимости от диаметра провода (троса) |
| 10 | 1,0 |
| 20 | 0,9 |
| 30 | 0,8 |
| 50 | 0,7 |
| 70 | 0,6 |
Примечание. Для промежуточных высот и диаметров значения коэффициентов Ki и Kd определяются линейной интерполяцией. Нормативную толщину стенки гололеда плотностью 0,9 г/см3 следует принимать по табл. в соответствии с картой районирования территории России по толщине стенки гололеда или по региональным картам районирования.
Карта районирования территории РФ по толщине стенки гололеда. Детальнее смотрите в интерактивных климатических картах.
Нормативная толщина стенки гололеда bэ для высоты 10 м над поверхностью земли:
| Район по гололеду | Нормативная толщина стенки гололеда bэ, мм |
| I | 10 |
| II | 15 |
| III | 20 |
| IV | 25 |
| V | 30 |
| VI | 35 |
| VII | 40 |
| Особый | Выше 40 |
2.8. Ветровая нагрузка на кабель при гололёде
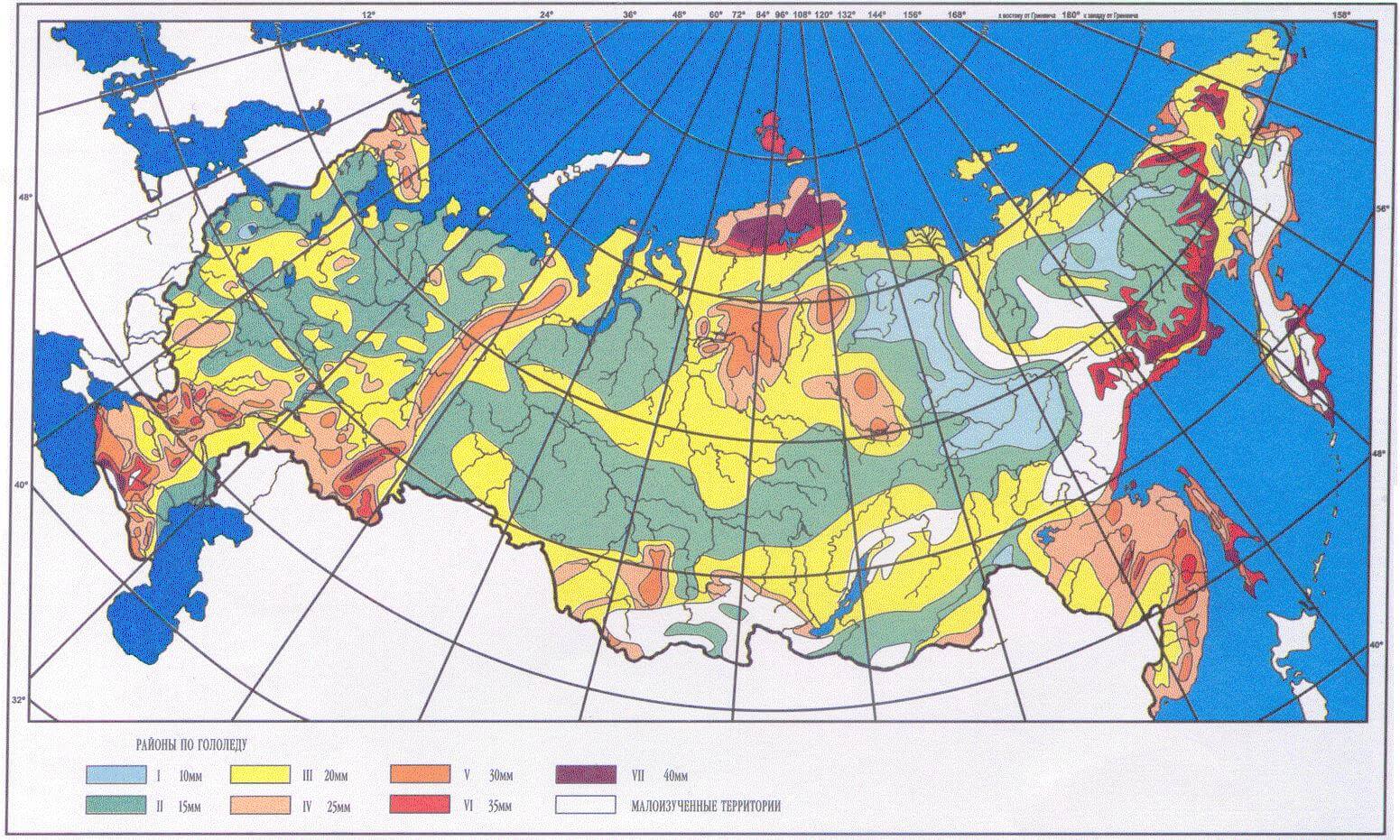
Также необходимо учитывать, что в процессе эксплуатации на подвешенный оптический кабель действуют ветровые нагрузки и следует рассчитать максимальную нагрузку под воздействием ветра. Для этого, исходя из географического места подвеса кабеля, по классификации и картам районов РФ по максимальной ветровому давлению (или скорости ветра), выбирают необходимое значение.
Детальнее смотрите в интерактивных климатических картах.
Ветровая нагрузка действует на кабель в горизонтальном направлении, перпендикулярном его оси.
Ветровая нагрузка (Н/м) рассчитывается следующим образом:
где aw — коэффициент, учитывающий неравномерность ветрового давления по пролету ВЛ, принимаемый равным:
| Ветровое давление, Па | До 200 | 240 | 280 | 300 | 320 | 360 | 400 | 500 | 580 и более |
| Коэффициент aw | 1 | 0,94 | 0,88 | 0,85 | 0,83 | 0,80 | 0,76 | 0,71 | 0,70 |
Промежуточные значения aw определяются линейной интерполяцией; Kl — коэффициент, учитывающий влияние длины пролета на ветровую нагрузку, равный 1,2 при длине пролета до 50 м, 1,1 — при 100 м, 1,05 — при 150 м, 1,0 — при 250 м и более (промежуточные значения Kl определяются интерполяцией); Kw — коэффициент, учитывающий изменение ветрового давления по высоте в зависимости от типа местности, определяемый по таблице:
| Высота расположения приведенного | Коэффициент Kw для типов местности | ||
| центра тяжести проводов, тросов и средних точек зон конструкций опор ВЛ над поверхностью земли, м | А | В | С |
| До 15 | 1,00 | 0,65 | 0,40 |
| 20 | 1,25 | 0,85 | 0,55 |
| 40 | 1,50 | 1,10 | 0,80 |
| 60 | 1,70 | 1,30 | 1,00 |
| 80 | 1,85 | 1,45 | 1,15 |
| 100 | 2,00 | 1,60 | 1,25 |
| 150 | 2,25 | 1,90 | 1,55 |
| 200 | 2,45 | 2,10 | 1,80 |
| 250 | 2,65 | 2,30 | 2,00 |
| 300 | 2,75 | 2,50 | 2,20 |
| 350 и выше | 2,75 | 2,75 | 2,35 |
По условиям воздействия ветра на ВЛ различают три типа местности:
- А — открытые побережья морей, озер, водохранилищ, пустыни, степи, лесостепи, тундра.
- В — городские территории, лесные массивы и другие местности, равномерно покрытые препятствиями высотой не менее 2/3 высоты опор.
- С — городские районы с застройкой зданиями высотой более 25 м, просеки в лесных массивах с высотой деревьев более высоты опор, орографически защищенные извилистые и узкие склоновые долины и ущелья.
Cx — коэффициент лобового сопротивления, принимаемый равным: 1,1 — для кабелей, свободных от гололеда, диаметром 20 мм и более; 1,2 — для всех кабелей, покрытых гололедом, и для всех проводов и тросов, свободных от гололеда, диаметром менее 20 мм;
W — нормативное ветровое давление, Па, в рассматриваемом режиме:
- в режиме максимального ветра: W = W0 — определяется по табл. в зависимости от ветрового района:
| Район по ветру | Нормативное ветровое давление W0, Па (скорость ветра v0, м/с) |
| I | 400 (25) |
| II | 500 (29) |
| III | 650 (32) |
| IV | 800 (36) |
| V | 1 000 (40) |
| VI | 1 250 (45) |
| VII | 1 500 (49) |
| Особый | Выше 1 500 (выше 49) |
- в режиме максимального гололеда: W = Wг — определяется, следующим образом: Нормативное ветровое давление при гололеде Wг с повторяемостью 1 раз в 25 лет определяется по скорости ветра при гололеде vг. Скорость ветра vг принимается по региональному районированию ветровых нагрузок при гололеде или определяется по данным наблюдений согласно методическим указаниям по расчету климатических нагрузок. При отсутствии региональных карт и данных наблюдений Wг = 0,25 W0.
Если в исходных данных известна скорость ветра v0, то ветровое давление (Па) определяется следующим образом:
2.9. Максимальная нагрузка, действующая на кабель
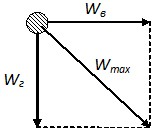
Совместное действие вертикальной гололедной нагрузки и горизонтальной ветровой определяется как максимальная нагрузка по следующей формуле:
2.10. Расчет максимальной стрела провеса
2.10.1. Определив максимальную нагрузку, можно узнать длину кабеля в нагруженном состоянии (из п. 2.5. и п. 2.2.):
2.10.2. Эта же величина равна:
2.10.3. Из п.п. 2.2. и 2.4.
2.10.4. Подставив выражения из 2.10.3. в 2.10.2. получим:
2.10.5. Из п.2.4 находим:
Тогда:
2.10.6. Подставим выражение из п.2.10.5. в выражение из п.2.10.4.:
2.10.7. Приравняем выражения из 2.10.1. и 2.10.6.:
После преобразования, получим кубическое уравнение следующего вида:
2.10.8. Т. е.:
где:
2.10.9. Решив кубическое уравнение можно получить значения максимальной стрелы провеса при наиболее сложных погодных условиях:
Если
то:
Если
то:
2.11. Максимальная растягивающая нагрузка при наихудших условиях
Зная максимальную стрелу провеса кабеля, легко найти (по аналогии с п. 2.2.) максимальную растягивающую нагрузку, действующую на кабель, при наихудших погодных условиях:
Эквивалентные пролеты и стрелы провеса при переде высот между опорами рассчитываются по аналогии с п. 2.3, только вместо начального веса и нагрузки подставляются максимальный вес и максимальная нагрузка:
2.12. Расчет монтажной стрелы провеса, нагрузки и монтажной таблицы
По п. 2.6. определяется длина кабеля в ненагруженном состоянии с учетом монтажной температуры:
Далее расчет ведется, согласно п.п. 2.10.8, 2.10.9 и 2.11 подставляя соответствующую длину кабеля в ненагруженном состоянии (Lн.монT), модуль упругости кабеля Eкаб и вес кабеля W и определяется стрела провеса при соответствующей температуре монтажа (Sмон) и нагрузка (Hмон).
Монтажная таблица стрел провеса — монтажные нагрузки и стрелы провеса при различных температурах монтажа исходя из заданной начальной нагрузки. Расчет монтажной таблицы ведется аналогично расчету максимальной нагрузки и стрел. Определяется длина кабеля в ненагруженном состоянии при различной температуре:
где Тмон – температура кабеля в условиях эксплуатации; Тср – средняя температура эксплуатации. Эта длина используется при расчете коэффициентов для определения монтажной стрелы провеса, в качестве веса используется вес кабеля в нормальных условиях:
По рассчитанным коэффициентам вычисляется Sмон и Hмон, согласно п. 2.10.9 и 2.11.
2.13. Расчет конечной стрелы провеса и нагрузки при нормальных условиях
После воздействия на кабель максимально тяжелого режима (гололед с ветром), кабель возвращается (сжимается) в нормальное состояние по конечному модулю упругости, т. е. остается остаточное удлинение (см. п. 1.7). Для того чтобы рассчитать конечную стрелу провеса и нагрузку при нормальных условиях необходимо определить длину кабеля при воздействии максимальной нагрузки:
Далее эта длина приводится к длине кабеля в ненагруженном состоянии по конечному модулю упругости:
Затем по п.п. 2.10.8, 2.10.9 и 2.11 (подставляя W, Lкк, Eкон) находим конечную стрелу провеса Sн.кон и нагрузку Hн.кон. Эквивалентные длины пролетов и стрел провеса (при наличии перепада высот между опорами) определяются согласно п. 2.3., подставляя вес кабеля и рассчитанную нагрузку.
2.13. Расчет стрелы провеса и нагрузки при нормальных условиях после реализации вытяжки
В процессе эксплуатации кабеля при подвесе происходит его вытяжка (см. п.1.8). Для того, чтобы определить стрелу провеса Sн.выт и нагрузку Hн.выт после вытяжки, необходимо воспользоваться формулами из п.п. 2.10.8, 2.10.9 и 2.11, подставляя в коэффициент b вместо начального модуля упругости, модуль упругости после вытяжки Eвыт. Вес принимается равным весу кабеля. Эквивалентные длины пролетов L1н.выт, L2н.выт и стрел провеса S1н.выт, S2н.выт (при наличии перепада высот между опорами) определяются согласно п. 2.3., подставляя вес кабеля и рассчитанную нагрузку.
2.14. Расчет стрел провеса и нагрузок при минимальной и максимальной температуре эксплуатации после реализации вытяжки
По п. 2.6. определяется длина кабеля в ненагруженном состоянии с учетом минимальной или максимальной температуры:
Далее расчет ведется, согласно п.п. 2.10.8, 2.10.9 и 2.11 подставляя соответствующую длину кабеля в ненагруженном состоянии (Lн minT, Lн maxT), модуль упругости вытяжки Eвыт и вес кабеля W и определяется стрела провеса при соответствующей температуре (Sн minT, Sн minT) и нагрузки (Hн minT , Hн maxT).
2.15. Расчет стрелы провеса и нагрузки при максимальных условиях (гололед + ветер) после реализации вытяжки
Определяется длина кабеля между опорами по п. 2.4. подставляя соответствующие значения эквивалентных пролетов и стрел провеса после вытяжки в нормальных условиях (по п. 2.4):
Затем определяется длина кабеля в ненагруженном состоянии (по конечному модулю упругости) по п.2.5.:
С учетом температуры:
Далее расчет ведется, согласно п.п. 2.10.8, 2.10.9 и 2.11 подставляя соответствующую длину кабеля после вытяжки (Lк.каб.выт), конечный модуль упругости Eкон, максимальную нагрузку Wmax (из п. 2.9) и определяется стрела провеса при максимальных нагрузках после вытяжки (Smax выт) и нагрузка (Hmax выт). Эквивалентные длины пролетов L1 max выт, L2 max выт и стрел провеса S1 max выт, S2 max выт (при наличии перепада высот между опорами) определяются согласно п. 2.3., подставляя максимальную нагрузку Wmax и рассчитанную растягивающую нагрузку Hmax выт.
Воспользуйтесь нашим конфигуратором подвесных ВОЛС. С его помощью вы сможете автоматически:
- рассчитать нагрузки и стрелы провеса кабеля при максимальных воздействиях льда и ветра, а также подготовить монтажные таблицы;
- рассчитать эллипсы пляски кабеля для исключения их схлестывания с проводами;
- подобрать рекомендуемые строительные длины кабеля в зависимости от мест расстановки муфт и длины трассы.
2.16. Определение роли вытяжки при расчете максимальных нагрузок
Если при воздействии максимальных нагрузок на кабель (гололед и ветер), растягивающая нагрузка после реализации вытяжки (по п. 2.15) будет больше растягивающей нагрузки на кабель не подвергшийся вытяжке (по п. 2.11):
то в таком случае вытяжка является определяющим фактором и при расчетах необходимо учитывать стрелы провеса и нагрузки, возникающие после реализации вытяжки (по п. 2.15). Если же максимальная растягивающая нагрузка после вытяжки (по п. 2.15) меньше максимальной растягивающей нагрузки без учета вытяжки (по п. 2.11):
то в таком случае вытяжка НЕ является определяющим фактором и при расчетах необходимо учитывать стрелы провеса и нагрузки, возникающие после первоначального удлинения кабеля (по п. 2.11).
2.17. Расчет стрелы провеса и нагрузки при воздействии максимального гололеда
Для того, чтобы определить максимальную вертикальную стрелу провеса Smax.вер. и нагрузку Hmax.вер, необходимо воспользоваться формулами из п.п. 2.10.8, 2.10.9 и 2.11, подставляя Lк.каб.выт и Eкон (если вытяжка — фактор) или Lнк и Eнач (если вытяжка — не фактор). Вес принимается равным весу кабеля под воздействием гололеда Wг (по п. 2.7). Эквивалентные длины пролетов L1г, L2г и стрел провеса S1г, S2г (при наличии перепада высот между опорами) определяются согласно п. 2.3., подставляя вес кабеля под воздействием льда и рассчитанную нагрузку Hmax.вер.
2.18. Расчет стрелы провеса и нагрузки при воздействии максимальной силы ветра
Максимальная ветровая нагрузка, действующая на кабель определяется по п. 2.8:
При этом используется максимальное ветровое давление W0 и диаметр кабеля dкаб без воздействия гололеда. Если максимальная ветровая нагрузка при воздействии гололеда Wв (по п.2.8) больше максимальной ветровой нагрузки без гололеда Wв max:
то тогда для данного режима берется ветровая нагрузка при гололеде:
Для того, чтобы определить максимальную горизонтальную стрелу провеса Smax.гор. и нагрузку Hmax.гор, необходимо воспользоваться формулами из п.п. 2.10.8, 2.10.9 и 2.11, подставляя Lк.каб.выт и Eкон (если вытяжка — фактор) или Lнк и Eнач (если вытяжка — не фактор). Вес принимается равным весу кабеля под воздействием максимального ветра Wв max. Эквивалентные длины пролетов L1в, L2в и стрел провеса S1в, S2в (при наличии перепада высот между опорами) определяются согласно п. 2.3., подставляя вес кабеля под воздействием ветра Wв max и рассчитанную нагрузку Hmax.вер.
2.19. Проверка допустимости расчетных значений заданным условиям
Результаты расчетов должны быть проверены на допустимость заданным условиям (в тех частях, где они заданы): Максимальная растягивающая нагрузка на кабель не должна превышать допустимую:
Максимальная вертикальная стрела провеса не должна превышать допустимую:
Минимальное расстояние от кабеля (при максимальной вертикальной стреле) до земли не должно быть меньше допустимого:
Монтажная нагрузка не должна превышать максимально допустимую монтажную нагрузку:
И другие проверки согласно заданным условиям.
3.1. Расчет стрелы провеса на произвольном расстоянии от одной из опор
Для того, чтобы рассчитать стрелу провеса на любом расстоянии от одной из опор, достаточно воспользоваться следующей формулой:
Где y — расстояние от более высокой опоры, S2, L2 — эквивалентная стрела провеса и расстояние для более высокой опоры, Sy — стрела провеса на заданном расстоянии от более высокой опоры.
3.2. Расчет монтажной таблицы для других расстояний между опорами при заданной начальной стреле провеса или нагрузке
Если задана начальная стрела провеса, то начальная нагрузка рассчитывается по п. 2.2, подставляя требуемое расстояние между опорами Lx. Если задана начальная нагрузка, то начальная стрела провеса определяется из формулы по п. 2.2:
Далее расчёт ведется по п.п. 2.3–2.6 и 2.12.

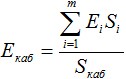
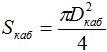

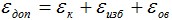
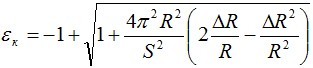
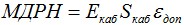
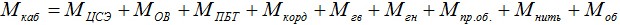
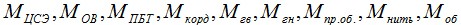
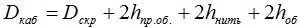
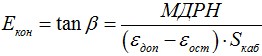
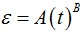
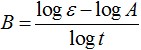
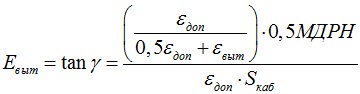
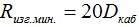
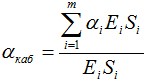
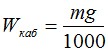
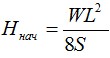
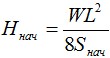
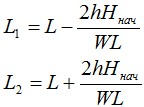
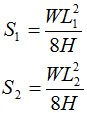
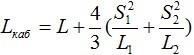
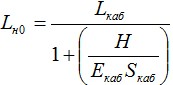
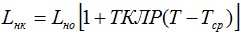
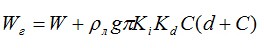
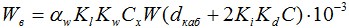
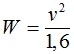
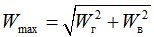
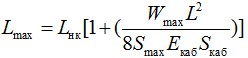
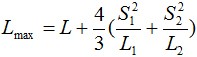
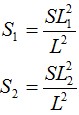
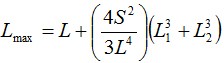
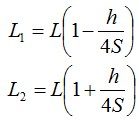
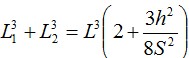
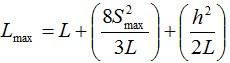
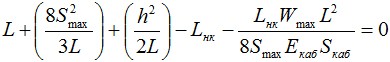
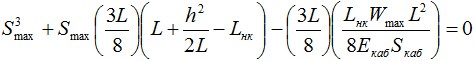
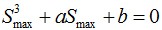
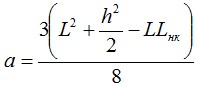
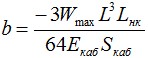
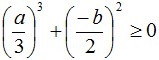
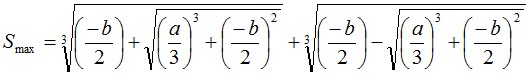
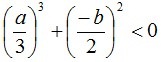
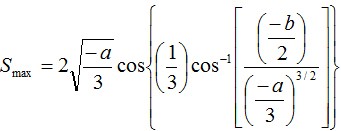
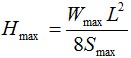
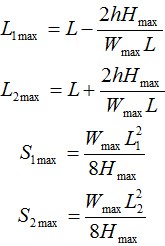
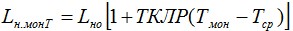
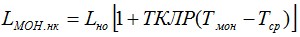
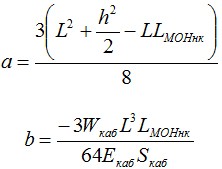
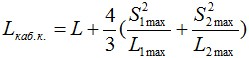
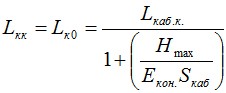
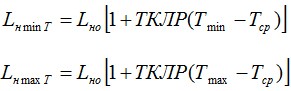
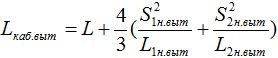
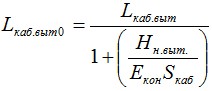
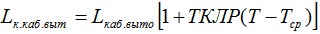
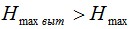
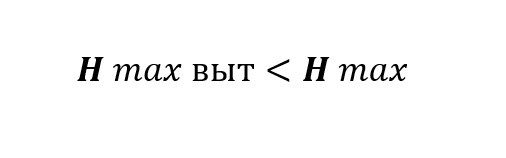
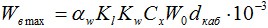
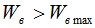
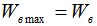
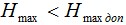
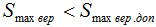
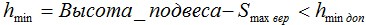
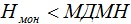
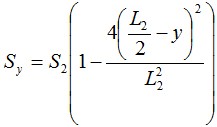
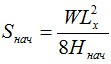

по пункту 2.5. Длина кабеля в ненагруженном состоянии, если H=0, на выходе получается Lкаб/1 = L каб… как это решается? для чего это нужно
Андрей, ключевая фраза здесь: “как ЕСЛИ БЫ он не находился под действием растягивающих нагрузок”. Если 100 метров кабеля просто положить на землю, то да: у вас будет Lкаб/1=Lкаб. Но мы 100 метров кабеля подвесили между опорами и он растянулся. Длина стала, к примеру 100,1 м. Именно эта длина (Lкаб) и считается в 2.4. А нам надо найти исходную длину кабеля для дальнейших расчетов. Поэтому в формулу 2.5 мы вставляем текущую нагрузку Н (а не нулевую), далее считаем длину с учетом температуры в 2.6. И в 2.10 используем именно эти величины, а не Lkab.
Здравствуйте! Возможно выложить расчет по реальному примеру?