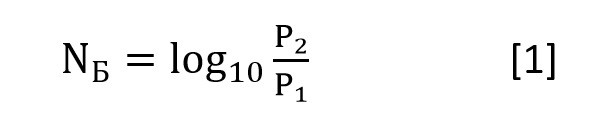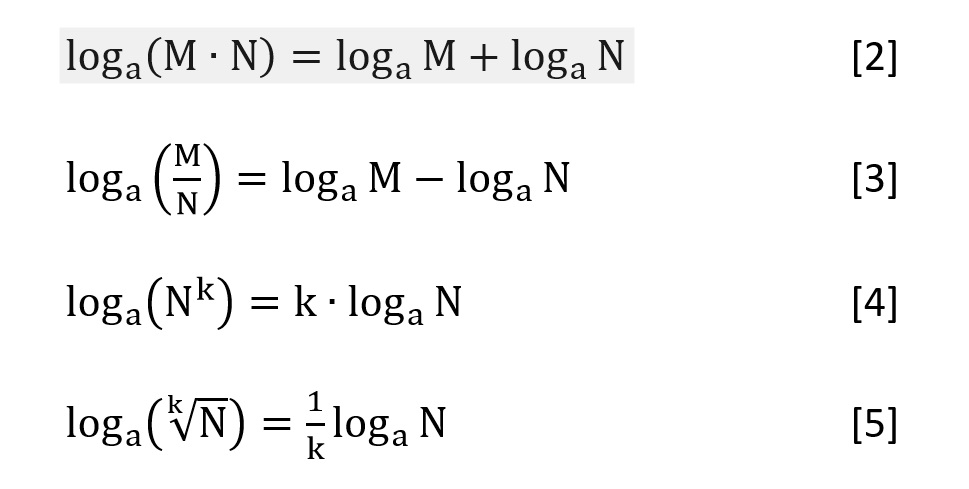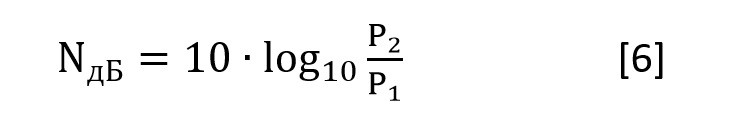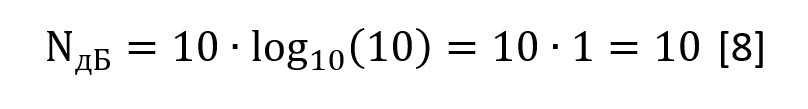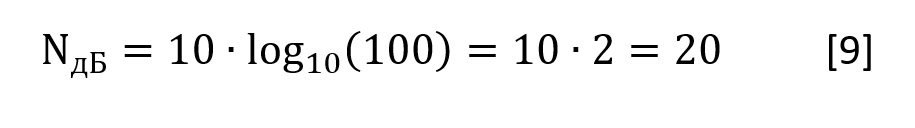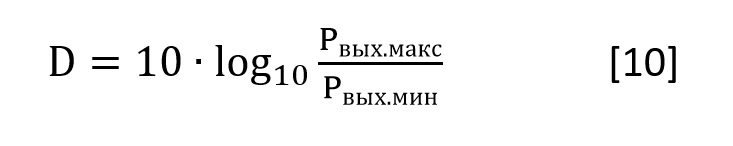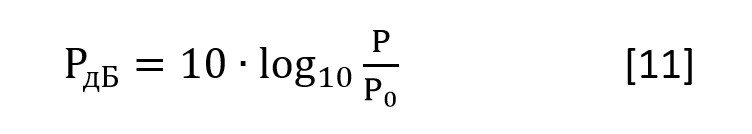Децибелы (русское обозначение — дБ, международное — dB) можно использовать для измерения или выражения отношения однородных энергетических величин, таких как мощность, энергия, интенсивность, плотность потока мощности, спектральная плотность мощности и т. п., а также силовых величин, таких как напряжение, сила тока, напряженность поля, звуковое давление и т. п.
Часто в качестве одной из величин отношения (в знаменателе) выступает общепринятая исходная (или опорная) величина. Тогда отношение, выраженное в децибелах, принято называть уровнем соответствующей физической величины (например, уровень мощности, уровень напряжения и т. д.).
В данном материале ограничимся подробным изложением применения этих единиц касательно характеристик ВОЛС — для сравнения мощностей. А конкретней — мощности оптического излучения.
Итак, децибел — не физическая величина, а математическое представление.
В этом отношении у децибел есть сходство с процентами — как и проценты, децибелы безразмерны и служат для сравнения двух величин, в принципе самых различных, независимо от их природы.
Децибел составляет десятую часть более крупной единицы — бела. Бел — это десятичный логарифм отношения двух мощностей. Если известны две мощности Р1 и Р2, то их отношение, выраженное в белах, определяется формулой:
Повторим ещё раз, что физическая природа сравниваемых мощностей может быть любой! Электрической, электромагнитной, акустической, механической, — важно лишь, чтобы обе величины были выражены в одинаковых единицах — ваттах, милливаттах и т. п.
Напомним вкратце, что такое логарифм. Любое положительное число, как целое, так и дробное, можно представить другим числом в определенной степени.
Так, например, если 102 = 100, то 10 называют основанием логарифма, а число 2 — логарифмом числа 100 и обозначают log10 100=2 или, в более компактной записи, lg 100 = 2 (читается так: «логарифм ста при основании десять равен двум»).
Логарифмы с основанием 10 называются десятичными логарифмами и применяются чаще всего. Для чисел, кратных 10, этот логарифм численно равен количеству нулей за единицей, а для остальных чисел вычисляется на калькуляторе или находится по таблицам логарифмов.
Основные свойства логарифмов представлены на изображении ниже:
Разумеется, эти свойства справедливы и для десятичных логарифмов. Логарифмический способ представления чисел часто оказывается очень удобным, так как позволяет подменять умножение — сложением, деление — вычитанием, возведение в степень умножением, а извлечение корня — делением.
Прежде всего следует отметить удобство децибела по сравнению с единицей бел. Для практических применений бел оказался слишком крупной единицей, часто предполагающей дробную запись значения логарифмической величины. Поэтому для большей наглядности решили число, показывающее количество бел, умножать на 10 и полученное произведение считать показателем в децибелах, т. е., например, 3 Б = 30 дБ, 5,76 Б = 57,6 дБ и т. д.
Обычно отношение мощностей выражают сразу в децибелах по формуле:
Действия с децибелами не отличаются от операций с логарифмами.
Далее посчитаем, чему равно значение в дБ при определенном значении отношения в «разах». При этом предложим некоторые удобные даже для устного счёта значения.
Например, пусть P1 = P2. Чему будет равно их отношение? Правильно, оно будет равно 1. Вычисляем логарифм — в какую степень нужно возвести число 10, чтобы получить число 1? Зная, что любое число в степени 0 будет равно 1, отвечаем — нужно возвести в степень 0. Получим следующее:
Иными словами, для равных величин отличие будет составлять 0 дБ.
Теперь пусть P2 = 10∙P1. Это означает, что их отношение равно 10. Считаем логарифм:
Получается, что при отличии в 10 раз две величины будут иметь разницу в 10 дБ.
Сделаем то же самое для P1 и P2, отличающихся в 100 раз. Получаем:
Заметили тенденцию? Каждое прибавление «0» в числе раз приводит к увеличению на 10 дБ.
Если наши величины будут отличаться в миллион раз (1 000 000), то это будет равнозначно отличию на 60 дБ.
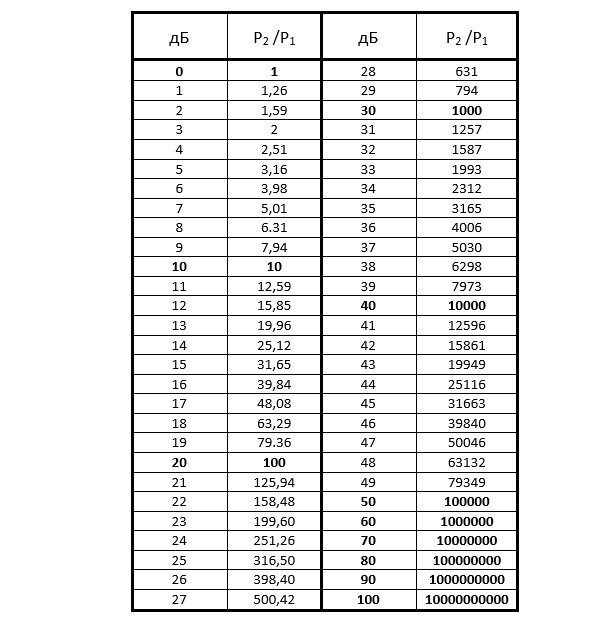
Разумеется, считать по этим формулам всякий раз, когда необходимо сделать такой перевод, очень затруднительно. Чтобы этим не заниматься, достаточно воспользоваться таблицами. При регулярном обращении к таким таблицам многие значения можно даже запомнить наизусть. Приведем одну из них ниже.
Табл.1. Перевод отношения мощностей в дБ
Подобным образом можно составить таблицу и для отрицательных значений децибел.
Нужно запомнить, что:
- Если P1 = P2. т. е. P2 / P1 = 1, то NдБ = 0.
- Если P2 > P1, то число децибел положительно.
- Если P2 < P1, то децибелы выражаются отрицательными числами.
Таким образом, можно сравнить два значения мощности и найти значение их разницы в дБ. Какие значения чаще всего нам придётся сравнивать для ВОЛС? Обычно речь идет о мощности, которая попадает на какой-то элемент или участок ВОЛС и мощности, которая выходит из него. Изменение мощности в данном случае будет наглядно сообщать об ослаблении или усилении сигнала. Чаще всего, разумеется, говорят об ослаблении уровня сигнала (если речь идет о пассивной части ВОЛС) или, по-другому, об оптических потерях.
Почему же используются именно логарифмы и децибелы, а не привычное всем соотношение в «разах»? Это удобно по ряду причин (перечисленные ниже удобства так или иначе связаны с применением не только децибелов, а логарифмической шкалы и логарифмических величин вообще):
- Характер отображения в органах чувств человека и животных изменений течения многих физических и биологических процессов пропорционален логарифму интенсивности раздражителя. Эта особенность делает применение логарифмических шкал, логарифмических величин и их единиц вполне естественным.
- Логарифмическая шкала дает наглядное графическое представление и упрощение анализа величины, изменяющейся в очень широких пределах. Огромные перепады преобразуемых чисел — от единиц и до миллионов — отображаются в децибелах числами первой сотни.
- Логарифмическое представление некоторых относительных величин в ряде случаев упрощает математические операции с ними, в частности умножение и деление заменяются сложением и вычитанием. Например, если собственные коэффициенты усиления последовательно включённых усилителей мощности выражены в децибелах, то общий коэффициент усиления находится как сумма собственных коэффициентов.
- Натуральные числа, представляющие степени десяти, выражаются в децибелах числами кратными десяти.
- Взаимообратные числа выражаются в децибелах равными числами, но с разными знаками.
Примеры применения децибел в описании параметров ВОЛС
Затухание сигнала в оптическом волокне
Потери мощности в линиях и кабелях на единицу длины характеризуются коэффициентом затухания α. Поскольку ОВ имеет свойство равномерно ослаблять мощность сигнала по мере прохождения его по волокну, можно говорить о величине «километрического затухания», т. е. сколько дБ мощности теряется в ОВ на единицу длины (километр) — дБ/км.
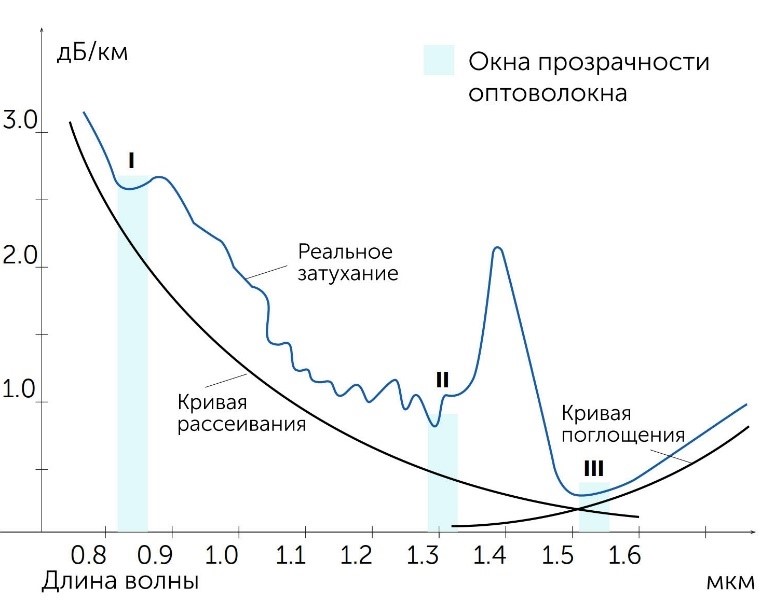
Величина эта зависит от длины волны излучения, которое распространяется в сердцевине волокна. График затухания сигнала в оптоволоконных кабелях показан на рис. 1:
Рис. 1. Диаграмма распределения километрического затухания в зависимости от длины волны
Динамический диапазон
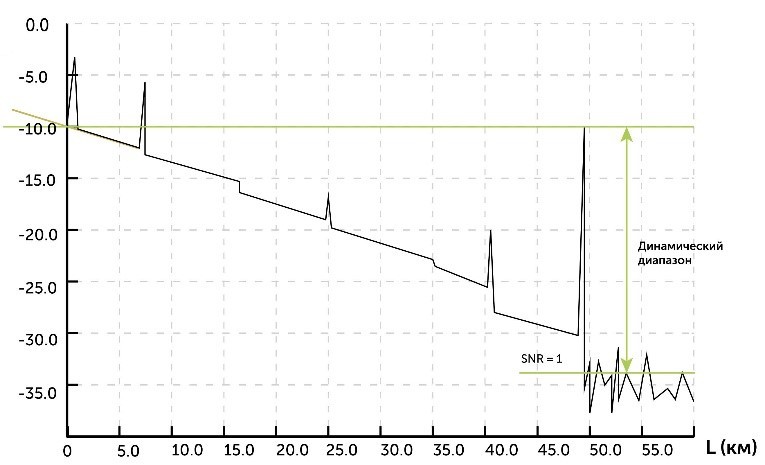
Динамическим диапазоном называется выраженное в децибелах отношение максимальной неискаженной выходной мощности к ее минимальному значению, при котором еще обеспечивается допустимое отношение сигнал/шум.
В сфере ВОЛС понятие динамического диапазона чаще всего встречается в характеристиках такого прибора, как оптический рефлектометр. По сути в этом случае динамический диапазон можно определить как разницу между уровнем ввода (на рефлектограмме) и верхней границей шумов (когда отношение сигнал/шум равно 1). Напомним, что с точки зрения измерителя динамический диапазон будет означать максимальную величину потерь в ВОЛС, которую способен корректно измерить конкретный рефлектометр. Иллюстрация к этому определению на рис.2:
Рис. 2. Динамический диапазон рефлектометра
Чем меньше уровень собственных шумов и чем выше неискаженная выходная мощность, тем шире динамический диапазон.
Представление абсолютной мощности в дБ
До сих пор мы полагали, что и числитель, и знаменатель (мощности P1 и P2) под знаком логарифма имеют произвольную величину и для выполнения децибельного пересчета важно знать только их отношение независимо от абсолютных значений.
В децибелах можно выражать также конкретные значения мощностей. Когда величина одного из членов, стоящих под знаком логарифма в рассмотренных ранее формулах задана, второй член отношения и числа децибел будут однозначно определять друг друга. Следовательно, если задаться какой-либо эталонной мощностью в качестве условного уровня сравнения, то другой мощности, сопоставляемой с ней, будет соответствовать строго определенное число децибел. Нулю децибел в этом случае отвечает мощность, равная мощности условного уровня сравнения. Этот уровень чаще всего называют опорным (или нулевым) — P0. Очевидно, что при разных опорных уровнях одна и та же конкретная мощность будет выражаться разными числами децибел.
где Р — мощность, подлежащая преобразованию в децибелы, а P0 — опорный уровень мощности. Величина P0 ставится в знаменателе, при этом положительными децибелами выражаются мощности Р > P0.
Условный уровень мощности, с которым производится сравнение, в принципе может быть любым, однако не каждый был бы удобен для практического использования. Чаще всего за опорный уровень выбирается мощность в 1 мВт.
Пользуясь формулой [11], легко найти, что относительно нулевого уровня 1 мВт мощность 1 Вт определяется как 30 дБ, 1 кВт как 60 дБ, а 1 МВт — это 90 дБ, т. е. практически все мощности, с которыми приходится встречаться в работе, укладываются в пределах первой сотни децибел. Мощности меньше 1 мВт будут выражаться отрицательными числами децибел.
Децибелы, определенные относительно уровня 1 мВт, называют децибел-милливаттом и обозначают дБм или dBm.
Использование такого представления мощности становится крайне удобным при использовании, например, оптического тестера. Получая при измерении значений двух мощностей (как правило, на входе в ВОЛС и на выходе из нее), выраженных в дБм, можно очень быстро получить разницу между ними в децибелах — она будет равна разности этих мощностей. А что из себя представляет такая разность? Это есть не что иное, как одна из самых важных характеристик любой волоконно-оптической сети — полные потери в оптическом волокне.